DP 10-2
Discovery Project ■ Computer Graphics III


Objective Learn how to rotate an image using rotation matrices.

In the Discovery Project Computer Graphics I we saw how matrix multiplication is used in computer graphics. We found matrices that reflect, expand, or shear an image. We now consider matrices that rotate an image, as in the graphics shown here.

Image of a hornbill perched upright on a bar.    Image of two hornbills, one perched upright on a bar and the second one inclined to the right.

Rotating Points in the Plane

Recall that a point $(x, y)$ in the plane is represented by the $2 \times 1$ matrix $\left[ \begin{array}{} x\\ y \end{array} \right]$. The matrix that rotates this point about the origin through an angle $ ɸ$ is $$R = \left[ \begin{array}{} \cos \; ɸ-\sin \; ɸ\\ \sin \; ɸ \;\;\; \cos \; ɸ \end{array} \right] \quad \color{#08F}{\textrm{Rotation} \; \textrm{matrix}}$$

Note that rotating a point counter-clockwise corresponds to rotating the axes clockwise.

When the point $P = \left[ \begin{array}{} x\\ y \end{array} \right]$ is rotated clockwise about the origin through an angle $ɸ$, it moves to a new location $P' = \left[ \begin{array}{} x'\\ y' \end{array} \right]$ given by the matrix product $P' = RP$, as shown in Figure 1.

The image shows a coordinate system with the x and y axes. A point P(x,y) is marked in the first quadrant on the graph, with a dashed line connecting it to the origin. Another point P′(x′,y′) is also marked in the first quadrant to the right of P, with an arc connecting P to P′. A rotation of the point P to P′ is shown by a curved arrow originating from the origin. The rotation angle phi is labeled at the intersection of the dashed lines. The point P is rotated counterclockwise around the origin to reach P′, as indicated by the arc and arrow.

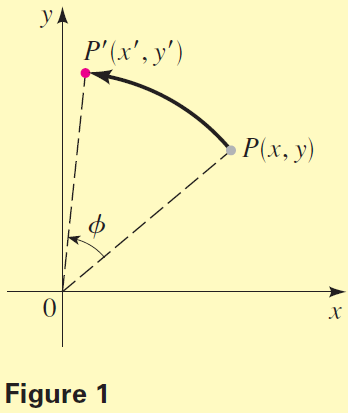
$$P' = RP = \left[ \begin{array}{} \cos \; ɸ-\sin \; ɸ\\ \sin \;ɸ \;\;\; \cos \; ɸ \end{array} \right] \left[ \begin{array}{} x\\ y \end{array} \right] = \left[ \begin{array}{} x \; \cos \; ɸ - y \; \sin \; ɸ\\ x \; \sin \; ɸ + y \; \cos \; ɸ \end{array} \right]$$

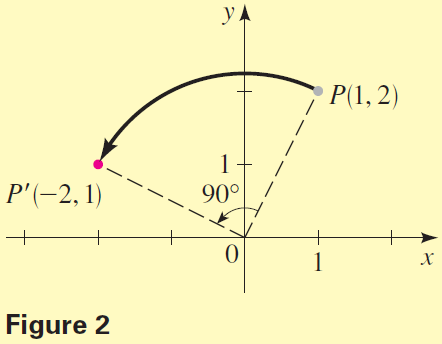
For example, if $ɸ = 90^\circ$, the rotation matrix is $$R = \left[ \begin{array}{} \cos \; 90^\circ &-\sin \; 90^\circ\\ \sin \; 90^\circ & \;\;\; \cos \; 90^\circ \end{array} \right] = \left[ \begin{array}{} 0&-1 \\ 1& \;\;\; 0 \end{array} \right] \quad \color{#08F}{\textrm{Rotation} \; \textrm{matrix} \; (ɸ = 90^\circ)}$$

Applying a $90^\circ$ rotation to the point $P = \left[ \begin{array}{} 1 \\ 2 \end{array} \right]$ moves it to the point $$P' = RP = \left[ \begin{array}{} 0&-1 \\ 1& \;\;\; 0 \end{array} \right]\left[ \begin{array}{} 1 \\ 2 \end{array} \right] = \left[ \begin{array}{} -2 \\ \;\;\; 1 \end{array} \right]$$

See Figure 2.

The image shows a coordinate system with the x and y axes. A grey point P(1,2) is marked on the graph, with a dashed line connecting it to the origin. Another pink point P′(negative 2,1) is marked on the graph with a dashed line connecting it to the origin. A curved arrow is shown from P to P′. and at the center between these two lines, a label of an angle of 90 degrees is shown.

Rotating Images in the Plane

If the rotation matrix is applied to every point in an image, then the entire image is rotated. To rotate the house in Figure 3(a) through a $30^\circ$ angle about the origin, we multiply its data matrix by the rotation matrix that has $ɸ = 30^\circ$.

$$RD = \left[ \begin{array}{} \frac{\sqrt 3}{2} & -\frac 12 \\ \frac 12 & \frac{\sqrt 3}{2} \end{array} \right] \left[ \begin{array}{} 2&0&0&2&4&4&3&3&2&2&3 \\ 0&0&3&5&3&0&0&2&2&0&0 \end{array} \right]$$ $$ \qquad \qquad \qquad \qquad \qquad \quad \approx \left[ \begin{array}{} 1.73&0&-1.50&-0.77&1.96&3.46&2.60&1.60&0.73&1.73&2.60 \\ \;\; 1&0& \;\;\; 2.60& \;\;\; 5.33&4.60& \;\; 2&1.50&3.23&2.73& \;\; 1&1.50 \end{array} \right]$$

The new data matrix $RD$ represents the rotated house in Figure 3(b).

Image (a): The image shows a coordinate system with the x and y axes. In the first quadrant, the figure of a pentagonal home is shown. The base of the home aligns with the x axis ranging in from 0 to 4. the left wall of the home aligns with y axis ranging from 0 to 3. The frame of the door has a width of 1 unit and a height of 2 units. Image (b): The image shows a coordinate system with the x and y axes. The figure of a pentagonal home is shown on the graph. The base of the home is slanted in the first quadrant and the left wall is slanted in the second quadrant.

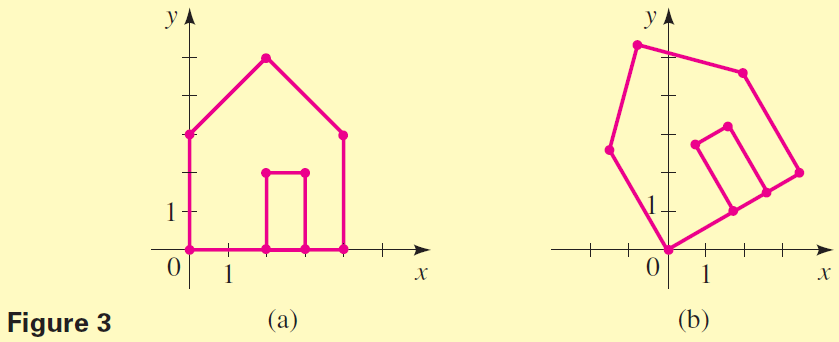
The Discovery Project: Computer Graphics II describes a TI-83 program that draws the image corresponding to a given data matrix. You may find it convenient to use this program in some of the following activities.

Problems
  1. Use a rotation matrix to find the new coordinates of the given point when it is rotated through the given angle.
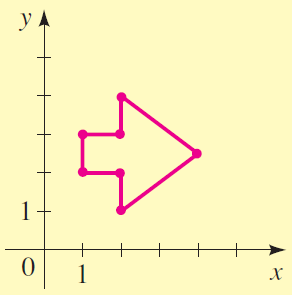
    (a) $(1, 4), \; ɸ = 90^\circ$   (b) $(-2, 1), \; ɸ = 60^\circ$
    (c) $(-2, -2), \; ɸ = 135^\circ$   (d) $(7, 3), \; ɸ = -60^\circ$
  2. Find a data matrix for the line drawing in the figure shown in the margin. Multiply the data matrix by a suitable rotation matrix to rotate the image about the origin by $ɸ = 120^\circ$. Sketch the rotated image given by the new data matrix.
    The image shows a coordinate system with the x and y axes. The figure of a right-pointing arrow is shown in the first quadrant.

  3. Sketch the image represented by the data matrix $D$. $$D = \left[ \begin{array}{} 2&3&3&4&4&1&1&2&2 \\ 1&1&3&3&4&4&3&3&1 \end{array} \right]$$
    Find the rotation matrix $R$ that corresponds to a $45^\circ$ rotation, and the transformation matrix $T$ that corresponds to an expansion by a factor of $2$ in the $x$-direction. How does multiplying the data matrix by $RT$ change the image? How about multiplying by $TR$? Calculate the products $RTD$ and $TRD$, and sketch the corresponding images to confirm your answers.
  4. Let $R$ be the rotation matrix for the angle $ɸ$. Show that $R^{-1}$ is the rotation matrix for the angle $- ɸ$.
  5. To translate an image by $(h, k)$, we add $h$ to each $x$-coordinate and $k$ to each $y$-coordinate of each point in the image (see the figure in the margin). This can be done by adding an appropriate matrix $M$ to $D$, but the dimension of $M$ would change depending on the dimension of $D$. In practice, translation is accomplished by matrix multiplication. To see how this is done, we introduce homogeneous coordinates; that is, we represent the point $(x, y)$ by a $3 \times 1$ matrix:

    $$(x, y) \leftrightarrow \left[ \begin{array}{cc|c} x \\ y \\ 1 \end{array} \right]$$

    The image shows a coordinate system with the x and y axes. Two copies of the figure of the face of a boy are placed in the first quadrant. The positioning indicated is as below. The chin of the left face has coordinates (x, y) and the chin of the right face has coordinates (x+h, y+k). The horizontal distance h between the two chins is indicated along the x axis and the vertical distance k is indicated along the y axis.

    1. Let $T$ be the matrix $$T = \left[ \begin{array}{} 1&0&h \\ 0&1&k \\ 0&0&1 \end{array} \right]$$
      Show that $T$ translates the point $(x, y)$ to the point $(x + h, y + h)$ by verifying the following matrix multiplication.
      $$\left[ \begin{array}{} 1&0&h \\ 0&1&k \\ 0&0&1 \end{array} \right]\left[ \begin{array}{} x \\ y \\ 1 \end{array} \right] = \left[ \begin{array}{} x + h \\ y + k \\ \;\;\; 1 \end{array} \right]$$
    2. Find $T^{-1}$ and describe how $T^{-1}$ translates points.

    3. Verify that multiplying by the following matrices has the indicated effects on a point $(x, y)$ represented by its homogeneous coordinates $\left[ \begin{array}{} x \\ y \\ 1 \end{array} \right].$ $$(i)\left[ \begin{array}{} 1& \; 0&0 \\ 0&-1&0 \\ 0& \; 0&1 \end{array} \right]\;\;\;\;(ii)\left[ \begin{array}{} c&0&0 \\ 0&1&0 \\ 0&0&1 \end{array} \right]\;\;\;\;(iii)\left[ \begin{array}{} 1&c&0 \\ 0&1&0 \\ 0&0&1 \end{array} \right]\;\;\;\;(iv)\left[ \begin{array}{} \cos \; ɸ-\sin \; ɸ &0 \\ \sin \; ɸ \;\;\; \cos \; ɸ &0 \\ \;\;\;0\;\;\;\;\;\;\;\;\;0&1 \end{array} \right]$$
      Reflection
      $\;$in $x$-axis      		   Expansion (or
      $\;$ contraction)
      $\;$in $x$-direction      		   $\;$Shear in
      $x$-direction      		   Rotation about the
      $\qquad$origin by
      $\; \quad$the angle $ɸ$

    4. Sketch the image represented (in homogeneous coordinates) by this data matrix: $$D = \left[ \begin{array}{} 3&5&5&7&7&9&9&7&7&5&5&3&3 \\ 7&7&5&5&7&7&9&9&11&11&9&9&7 \\ 1&1&1&1&1&1&1&1&1&1&1&1&1 \end{array} \right] $$
      Find a matrix $T$ that translates the image by $(-6, -8)$ and a matrix $R$ that rotates the image by $45^\circ$. Sketch the images represented by the data matrices $TD$, $RTD$, and $T^{-1}RTD$. Describe how an image is changed when its data matrix is multiplied by $T$, by $RT$, and by $T^{-1}RT$
      .