DISCOVERY PROJECT
Best Fit versus Exact Fit
Given several points in the plane, we can find the line that best fits them (the regression line). Of course, not all the points will necessarily lie on the line. We can also find the quadratic polynomial that best fits the points. Again, not every point will necessarily lie on the graph of the polynomial.
However, if we are given just two points, we can find a line of exact fit, that is, a line that actually passes through both points. Similarly, given three points (not all on the same line), we can find the quadratic polynomial of exact fit.
For example,suppose we are given the following three points: $$(-1, 6), \quad (1, 2), \quad (2, 3)$$
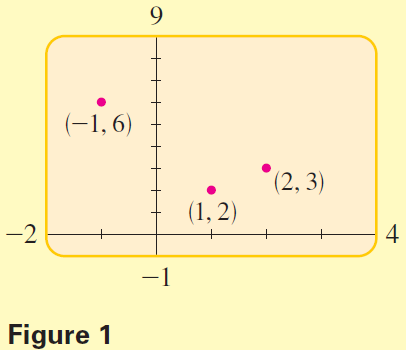
From Figure 1 we see that the points do not lie on a line. Let's find the quadratic polynomial that fits these points exactly. The polynomial must have the form $$y = ax^2 + bx + c$$
We need to find values for $a$, $b$, and $c$ so that the graph of the resulting polynomial contains the given points. Substituting the given points into the equation, we get the following.
| $(-1, 6)$ | $x = -1, \; y = 6$ | $6 = a(-1)^2 + b(-1) + c$ | ||
| $(1, 2)$ | $x = 1, \; y = 2$ | $2 = a(1)^2 + b(1) + c$ | ||
| $(2, 3)$ | $x = 2, \; y = 3$ | $3 = a(2)^2 + b(2) + c$ |
These three equations simplify into the following system. $$\begin{cases} a - b + c = 6 \\ a + b + c = 2 \\ 4a + 2b + c = 3 \end{cases} $$
Using Gaussian elimination we obtain the solution $a = 1$, $b = -2$, and $c = 3$.
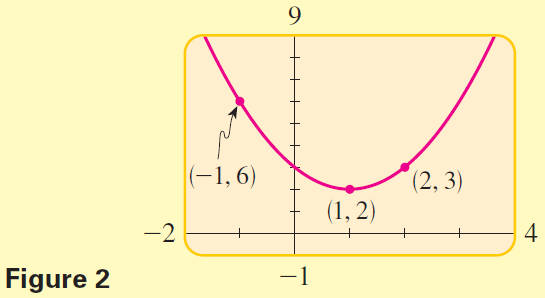
So the required quadratic polynomial is $$y = x^2 - 2x + 3$$
From Figure 2 we see that the graph of the polynomial passes through the given points.
- Find the quadratic polynomial $y = ax^2 + bx + c$ whose graph passes through the given points.
- $(-2, 3), (-1, 1), (1,9)$
- $(-1, -3), (2, 0), (3, -3)$
- Find the cubic polynomial $y = ax^3 + bx^2 + cx + d$ whose graph passes through the given points.
- $(-1, -4), (1,2), (2, 11), (3, 32)$
- $(-2, 10), (-1, 1), (1, -1), (3, 45)$
- A stone is thrown upward with velocity $v$ from a height $h$. Its elevation $d$ above the ground at time $t$ is given by $$d =at^2 + vt + h$$

The elevation is measured at three different times as shown.Time (s) $1.0$ $2.0$ $6.0$ Elevation (ft) $144$ $192$ $64$ - Find the constants $a$, $v$, and $h$.
- Find the elevation of the stone when $t = 4s$.
-
- Find the quadratic function $y = ax^2 + bx + c$ whose graph passes through the given points. (This is the quadratic curve of exact fit.) Graph the points and the quadratic curve that you found. $$(-2, 10), \; (1, -5), \; (2, -6), \; (4, -2)$$
- Now use the $\mathtt QuadReg$ command on your calculator to find the quadratic curve that best fits the points in part (a). How does this compare to the function you found in part (a)?
- Show that no quadratic function passes through the points $$(-2, 11), \; (1, -6), \; (2, -5), \; (4, -1)$$
- Use the $\mathtt QuadReg$ command on your calculator to find the quadratic curve that best fits the points in part (b). Graph the points and the quadratic curve that you found.
- Explain how the curve of exact fit differs from the curve of best fit.
