FOCUS ON PROBLEM SOLVING 4
One way to show that a statement is true is to show that its opposite leads to a contradiction. This type of indirect reasoning is an important problem-solving tool. The two examples we give here are problems that were solved over $2000$ years ago but continue to have a profound influence in mathematics.
Irrational Numbers Exist
The Pythagoreans were fascinated by the beauty of the natural numbers: $1, 2, 3 ….$ They hoped that the length of every interval constructed in geometry would be a ratio of two natural numbers, and so the natural numbers would describe all of geometry. But what is the length of the diagonal of a square of side $1$? They knew (by the Pythagorean Theorem) that this length is $\sqrt 2$. The question was: Is $\sqrt 2$ the ratio of two natural numbers? In other words, is $\sqrt 2$ a rational number? The Pythagoreans were able to prove that $\sqrt 2$ is not rational.
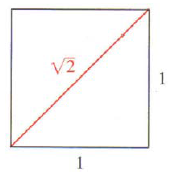
Suppose $\sqrt 2$ is rational, so that $$\sqrt 2 = \frac{a}{b}$$
where $a$ and $b$ are natural numbers with no factor in common. Then
| $\; a = \sqrt 2b \quad$ | $\color{#50F} {Multiply \; by \; b}$ |
| $a^2 = 2b^2 \quad$ | $\color{#50F}{Square}$ |
This means that $a^2$ is an even number and so $a$ is an even number. Then $a = 2m$, for some integer $m$. So the last equation leads to
| $(2m)^2 = 2b^2 \quad$ | $\color{#50F} {Because \; a = 2m}$ |
| $\; \; \; 4m^2 = 2b^2 \quad$ | $\color{#50F}{Square}$ |
| $\; \; \; 2m^2 = b^2 \quad$ | $\color{#50F}{Divide \; by \; 2}$ |
Thus $b$ is also even. So $a$ and $b$ have $2$ as a common factor and this contradicts our assumption that $a$ and $b$ have no factor in common. Thus the assumption that $\sqrt 2$ is rational leads to a contradiction and so $\sqrt 2$ must be irrational.
There are Infinitely Many Prime Numbers
A prime number is one that has no factors other than $1$ and itself. The first few primes are $$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . . .$$
How do we find the next prime? No formula is known that will produce the primes and no one has found a pattern for the location of the primes. One thing that is known is that there are infinitely many primes. Euclid gave a proof for this fact over $2000$ years ago by a brilliant use of indirect reasoning. Here is his famous proof:
Suppose that there are only a finite number of primes. We list them as $$p_1, p_2,…p_n$$
Then the number $$N = p_1. p_2. p_3. ….p_n+1$$
is not divisible by any prime (Why?) and so is itself prime. But $N$ is not in our list of primes (Why?). This contradicts our assumption that the list contained all the primes. Thus there are infinitely many primes.
PROBLEMS
- Prove that $\sqrt 3$ is irrational.
- Prove that $log_25$ is irrational.
- Evaluate $(log_23)(log_34)(log_45)…(log_{31}32)$.
- Show that if $x \gt 0$ and $x \neq 1$, then $$\frac {1}{log_2x} + \frac {1}{log_3x} + \frac {1}{log_5x} = \frac {1}{log_{30}x}$$
- Prove that at any party there are two people who know the same number of people. (Assume that if person $A$ knows person $B$ then $B$ knows $A$. Assume also that everyone knows himself or herself.)
- Prove that the number of people who have shaken hands an odd number of times is an even number.
- Suppose that each point in the plane is colored either red or blue. Show that there must always be two points of the same color that are exactly one unit apart.
- Suppose that each point $(x, y)$ in the plane, both of whose coordinates are rational numbers, represents a tree. If you are standing at the point $(0, 0)$, how far could you see in this forest?