FOCUS ON PROBLEM SOLVING 8

It is sometimes useful to attack a problem by first working backward. This means that we assume the conclusion and work backward step by step until we arrive at something that is given or known. Then we may be able to reverse the steps in the argument and proceed forward from the given information to the conclusion.

We have already used this procedure in solving equations. For example, in solving the equation $2x + 7 = 23$ we assume that $x$ is a number that satisfies $2x + 7 = 23$ and work backward. We subtract $7$ from each side of the equation and then divide each side by $2$ to get $x = 8$. Each of these steps can be reversed, so we have solved the problem.

Measuring Water

How is it possible to bring up from a river exactly $6$ gallons of water when you only have two containers, a $9$-gallon pail and a $4$-gallon pail?

SOLUTION

If you work this problem in the forward direction you might be lucky and discover, out of the many possibilities for proceeding, a correct solution. But it is more systematic to work backward.


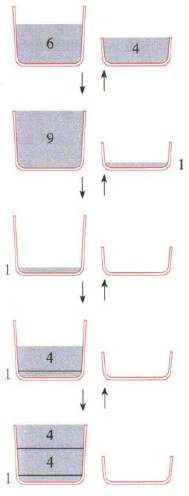
Imagine that we have $6$ gal of water in the $9$-gal pail, together with the full $4$-gal pail. We could fill the larger pail from the smaller one, leaving just $1$ gal in the smaller pail. Then we could empty the large pail and pour the $1$ gal of water into it. Finally we could exactly fill the larger pail by adding $8$ gal of water using the smaller pail twice.

Now, by reversing the procedure, we have the solution to the problem. Start with a full $9$-gal pail. Use it to fill the $4$-gal pail, then empty the $4$-gal pail. Again fill the $4$-gal pail from the larger one and empty the smaller one. This leaves $1$ gal in the larger pail. Transfer it to the smaller pail and fill the larger one. Use the larger pail to fill the smaller one. This leaves $6$ gal in the larger pail.

In the next example we combine the technique of working backward with the method of taking cases.

Solving an Absolute Value Equation

Solve the equation $|2x-|3x+1|| = 1$

SOLUTION

We assume that $x$ is a number that satisfies the equation. It follows .by properties of absolute value that there are two cases:


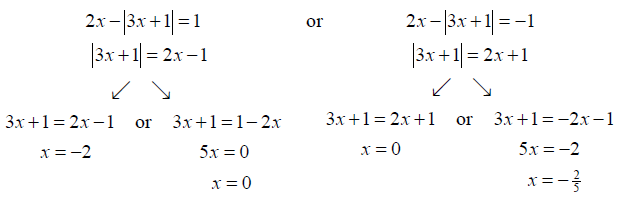
Thus working backward gives three potential solutions: $x = 0$, $x = -2$, $x = -\frac{2}{5}$. But is it possible to reverse the steps in each case? Let us check by trying to verify that these are indeed solutions:

Try $x = 0 : |2(0) - |3(0) +1|| = |0 -1| = 1 \quad\quad\quad\quad\quad\quad\quad \color{red}{0\; is\; a\; solution}$

Try $x = -2 : |2(-2) - |3(-2) +1|| = |-4 -5| = 9 \quad\quad \color{red}{-2\; is\; not\; a\; solution}$

Try $x = -\frac{2}{5} : |2(-\frac{2}{5}) - |3(-\frac{2}{5}) +1|| = |-\frac{4}{5} -\frac{1}{5}| = 1 \quad \color{red}{-\frac{2}{5}\; is\; a\; solution}$

Therefore the only solutions are $0$ and $-\frac{2}{5}$.

PROBLEMS
  1. Three containers hold $19$ gal, $13$ gal, and $7$ gal, respectively. The $19$-gallon contaier is empty. The other two are full. How can you measure out $10$ gal using no other container?
  2. Justin, Sasha, and Vanessa each have a bag of marbles. First Justin gives Sasha and Vanessa each as many marbles as they already have. Then Sasha gives Justin and Vanessa as many marbles as they now have. Finally, Vanessa gives Justin and Sasha as many marbles as they now have. Everyone ends up with $16$ marbles. How many did each person have to begin with?

    3. 3-6 Solve the equation

  3. $|5-|x-1|| = 3$
  4. $||2x+1|+5| = 10$
  5. $|4x-|x+1|| = 3$
  6. $||3x+1|-x| = 2$
  7. Draw the graph of the equation $|x| + |y| \le 1 + |xy|$.
  8. Sketch the region in the plane consisting of all points $(x, y)$ such that $$|x| + |y| \le 1$$
  9. Sketch the region in the plane consisting of all points $(x, y)$ such that $$|x-y| + |x| - |y| \le 2$$
  10. If $x$ and $y$ are positive real numbers, prove that $$\sqrt{xy} \le \frac{x+y}{2}$$
  11. Solve the following system of equations: $$\begin{cases} 3x + 5y + z + 7t = -8\\ 4x + 8y + 2z + 6t = -8\\ 6x + 2y + 8z + 4t = 8\\ 7x + y + 5z + 3t = 8 \end{cases} $$
    12. [Hint: Instead of immediately using the method of elimination, look for a shortcut.]
  12. Find the complete solution of the following system:$$\left\{ \begin{aligned} {x + y + z = 2}\\ x^2 + y^2 + z^2 = 2\\ {xy = z^2} \end{aligned} \right.$$