OBJECTIVE To explore how power functions model relationships between shape and size.

King Kong is "similar" to a normal $8$-foot ape but a lot bigger. In fact, he's just a blown up version of the real thing. So how does King Kong's shirt size or weight compare to that of a normal gorilla? In this exploration we investigate how areas and volumes of similar figures change as the size of the figure increases (or decreases). We'll find power functions that relate these quantities and use those functions to explore the possiblity of the existence of a real-life giant ape. We begin by finding some properties of similar figures.

I. Similar Objects

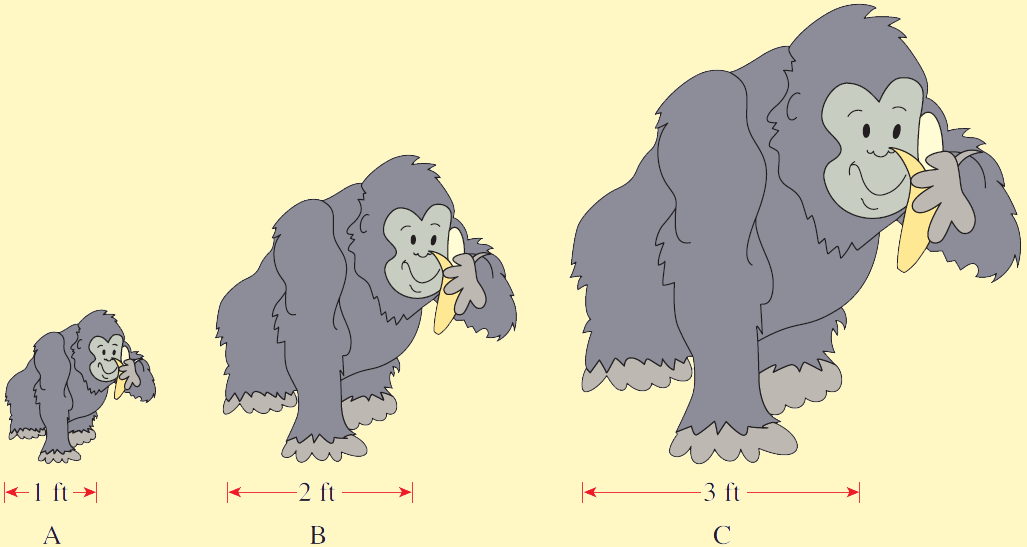
Two objects are similar if they have the same shape even though they may not be the same size. In geometry you learned that corresponding sides of similar triangles are proportional. This last property holds for any two similar figures, not just triangles. For example, the gorillas in the figures below are all similar. Gorilla C is three times as tall as Gorilla A, so Gorilla C's hand is three times as long, his eyes are three times as far apart, his feet are three times as long, and so on. The figures "look the same" precisely because they are similar in the mathematical sense.

The scaling factor of two similar figures is the ratio of the distance between corresponding points. So the scaling factor between Gorillas C and A is $3$. This means that if two points are a distance $x$ apart in Gorilla A, then the corresponding points are a distance $3x$ apart in Gorilla C. (We can also say that the scaling factor between gorillas A and C is $\frac{1}{3}$.)

1. Find the following scaling factors:
   1. The scaling factor between Gorillas B and A is _______.
   2. The scaling factor between Gorillas A and B is _______.
   3. The scaling factor between Gorillas B and C is _______.
2. Is a map of Chicago similar to the city of Chicago? How are distances on the map related to actual distances in the city? Is the scaling factor indicated on the map?
3. How is your photograph similar to you? Compare distances between your eyes, ears, length of nose, and so on to the corresponding distances in the photograph. What is the scaling factor?
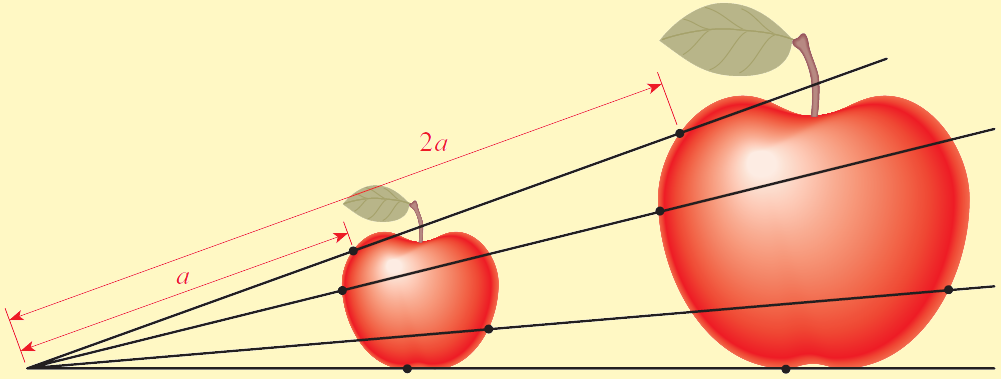
4. The figure illustrates a method of drawing an apple twice the size of a given apple. Use the method to draw an apple one-third the size of the bigger apple shown here.
   
   
   

II. Areas of Similar Objects

If two objects are similar, then how are their areas related? First, let's see what happens if the objects are squares.

1. 
   
   
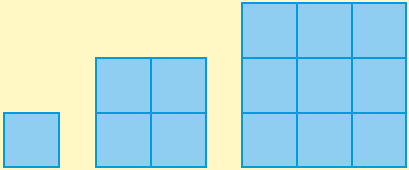
   Look at the above squares to help answer the following questions.
   1. If the side of a square is doubled, then its area is multiplied by _______.
   2. If the side of a square is tripled, then its area is multiplied by _______.
   3. If the side of a square is multiplied by $s$, then its area is multiplied by _______.
   4. Let's prove the conclusion you made in part (c) algebraically.
      • If a square has side $x$, then its area is $A_1$ = _______.
      • If a square has side $sx$, then its area is $A_2$ = _______.
      • Conclude that for any two squares with scaling factor $s$, their areas satisfy $A_2 = s^2 A_1$.
2. 
   
   
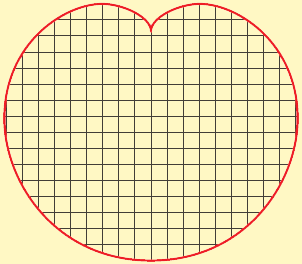
   A plane figure can always be approximated by small squares (as shown above). Use what you learned about areas of squares in Question 1 to explain why the following statement is true: For any two plane figures with scaling factor $s$, their areas satisfy $A_2 = s^2 A_1$.
3. Any surface, whether flat or not, can be approximated by squares, so the statement in Question 2 is true for any surface. Experiment with the surface areas of cubes and spheres as follows. (Use the cubes shown in Part III on the next page to help visualize the answer to part (a).)
   1. If the side of a cube is doubled, then the surface area of the cube is multiplied by _______.
   2. If the radius of a ball is doubled, then the surface area of the ball is multiplied by _______.
4. Suppose an irregularly shaped object (such as a gorilla) has surface area $A$. If the object is magnified $10$ times (scaling factor $10$), then the surface area of the magnified figure is _______.

III. Volumes of Similar Objects

If two objects are similar, then how are their volumes related? First, let's see what happens if the objects are cubes.

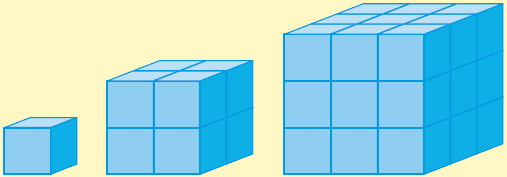
1. Look at the cubes above to help answer the following questions.
   1. If the side of a cube is doubled, then its volume is multiplied by _______.
   2. If the side of a cube is tripled, then its volume is multiplied by _______.
   3. If the side of a cube is multiplied by $s$, then its volume is multiplied by _______.
   4. Let's prove the conclusion you made in part (c) algebraically.
      • If a cube has side $x$, then its volume is $V_1$ = _______.
      • If a cube has side $sx$, then its volume is $V_2$ = _______.
      • Conclude that for any two cubes with scaling factor $s$, their volumes satisfy $V_2 = s^3V_1$.
2. A solid figure can be "filled" with little cubes. Use what you learned about volumes of cubes in Question 1 to explain why the following statement is true: For any two solid objects with scaling factor $s$, their volumes satisfy $V_2 = s^3V_1$.
3. Suppose an apple has volume $V$. If the apple is magnified $10$ times (scaling factor $10$), then the volume of the big apple is _______.

IV. Real-Life Giant Apes?

1. Let's suppose that King Kong is $10$ times as tall as Joe, a normal-sized gorilla. Of course, the two gorillas are similar.
   1. The scaling factor between King Kong and Joe is _______.
   2. If Joe's foot is $20$ inches long, then King Kong's foot is _______ inches long.
   3. If it takes $5$ square yards of material to make a shirt for Joe, then it takes _______ square yards of material to make a shirt for King Kong.
   4. If Joe weighs $500$ pounds, then King Kong weighs _______ pounds.
2. Your answer to Question 1(d) indicates that King Kong weighs half a million pounds. If he is made of normal flesh and blood, would his bones be able to support his weight? Or would his bones be crushed under his weight? In fact, no known substance is strong enough to withstand such enormous weight, so a living, moving gorilla of this size doesn't seem possible.