DISCOVERY PROJECT
Mapping the World
The method used to survey and map a town works well for small areas. But mapping the whole world would introduce a new difficulty: How do we represent the spherical world by a flat map? Several ingenious methods have been developed.
Cylindrical Projection
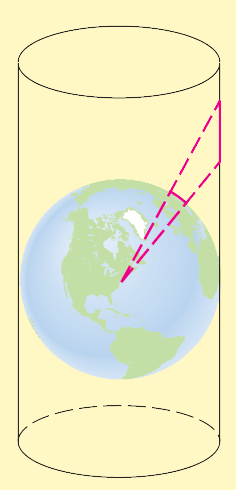
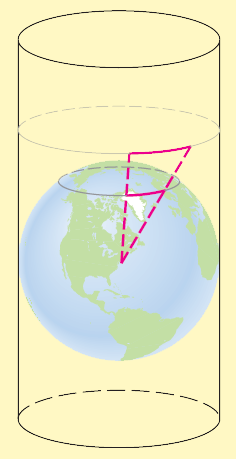
One method is the cylindrical projection. In this method we imagine a cylinder "wrapped" around the earth at the equator as in Figure 1. Each point on the earth is projected onto the cylinder by a ray emanating from the center of the earth. The "unwrapped" cylinder is the desired flat map of the world. The process is illustrated in Figure 2.
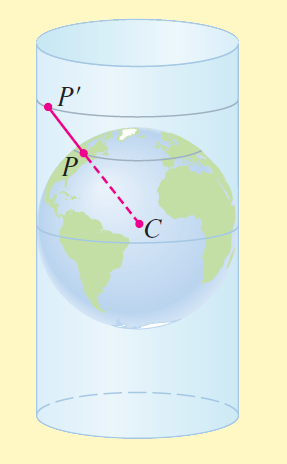
Figure 1: Point $P$ on the earth is projected onto point $P'$ on the cylinder by a ray from the center of the earth $C$.
Of course, we cannot actually wrap a large piece of paper around the world, so this whole process must be done mathematically, and the tool we need is trigonometry. On the unwrapped cylinder we take the $x$-axis to correspond to the equator and the $y$-axis to the meridian through Greenwich, England ($0^°$ longitude). Let $R$ be the radius of the earth and let $P$ be the point on the earth at $\alpha^°$ E longitude and $\beta^°$ N latitude. The point $P$ is projected to the point $P'(x,y)$ on the cylinder (viewed as part of the coordinate plane) where
| $x$ = $\left(\frac{\pi}{180}\right)$$\alpha$$R$ | Formula for length of a circular arc | |
| $y$ = $R$ $tan$ $\beta$ | Definition of tangent |
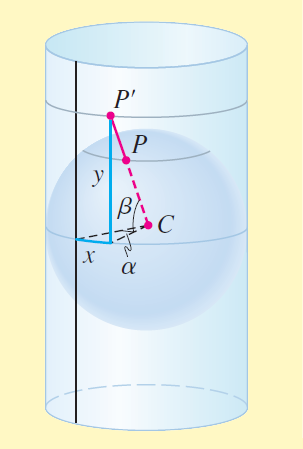
Figure 2a: Cylindrical projection
See Figure 2(a). These formulas can then be used to draw the map. (Note that West longitude and South latitude correspond to negative values of $\alpha$ and $\beta$, respectively.) Of course, using $R$ as the radius of the earth would produce a huge map, so we replace $R$ by a smaller value to get a map at an appropriate scale as shown in the figure.
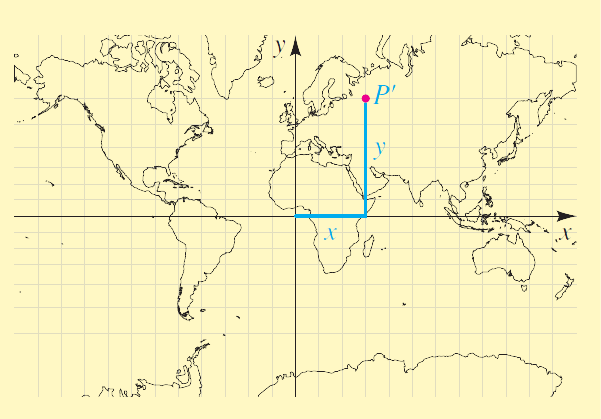
Figure 2b: Cylindrical projection map
Stereographic Projection
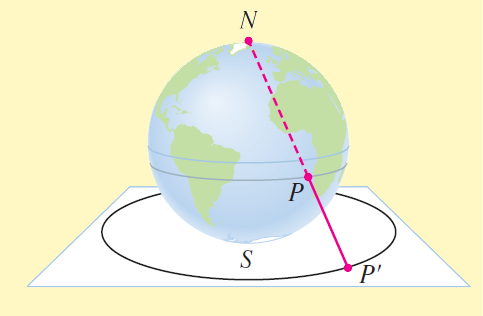
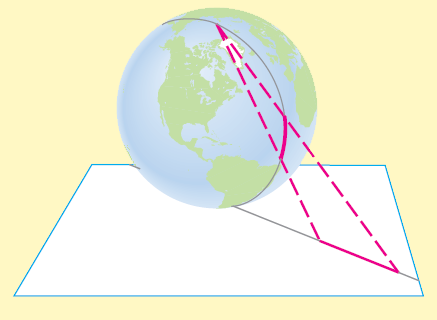
Figure 3: Point $P$ on the earth's surface is projected onto point $P'$ on the plane by a ray from the north pole.
In the stereographic projection we imagine the earth placed on the coordinate plane with the south pole at the origin. Points on the earth are projected onto the plane by rays emanating from the north pole (see Figure 3). The earth is placed so that the prime meridian ($0^°$ longitude) corresponds to the polar axis. As shown in Figure 4(a), a point $P$ on the earth at $\alpha^°$ E longitude and $\beta^°$ N latitude is projected onto the point $P'(r,θ)$ whose polar coordinates are
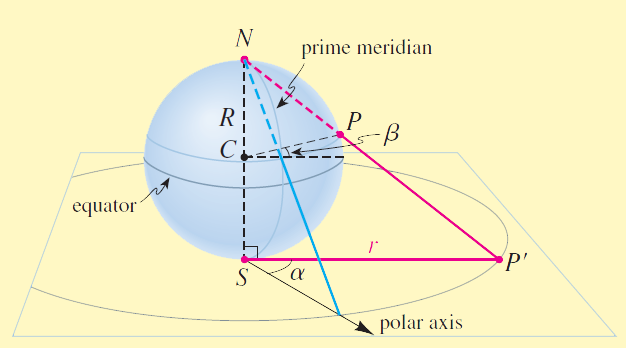
Figure 4a: Stereographic projection
| $r$ = $2R$ $tan\left(\frac{\beta}{2} + 45^°\right)$ | |
| $\theta$ = $\alpha$ |
Figure 4(b) shows how the first of these formulas is obtained
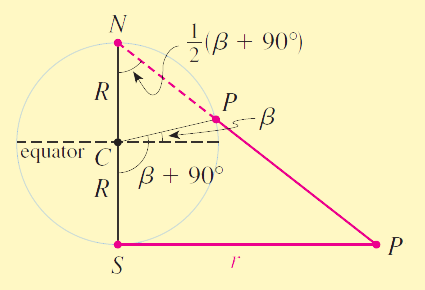
Figure 4b: Cross-section of stereographic projection
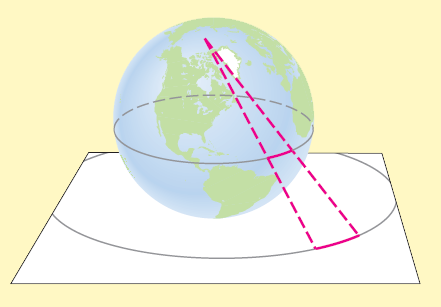
Figure 5 shows a stereographic map of the southern hemisphere.
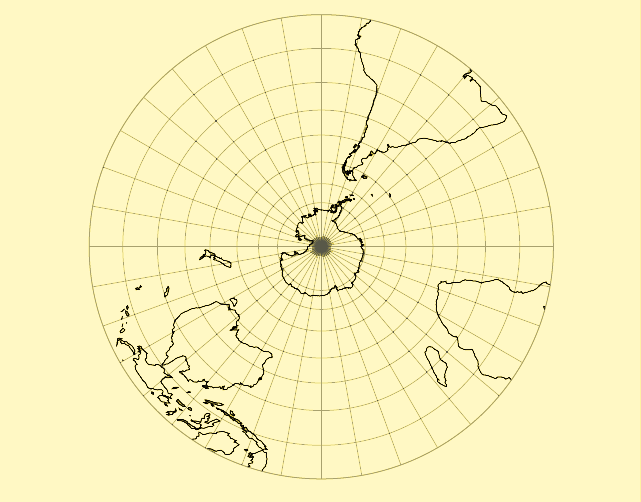
Figure 5: Stereographic projection of the southern hemisphere
Problems
- Cylindrical Projection A map maker wishes to map the earth using a cylindrical projection. The map is to be $36$ inches wide. Thus, the equator is mapped onto a horizontal $36$-inch line segment. The radius of the earth is $3960$ miles.
- What value of $R$ should he use in the cylindrical projection formulas?
- How many miles does one inch on the map represent at the equator?
- Cylindrical Projection To map the entire world using the cylindrical projection, the cylinder must extend infinitely far in the vertical direction. So a practical cylindrical map cannot extend all the way to the poles. The map maker in Problem 1 decides that his map should show the earth between $70^°$ N and $70^°$ S latitudes. How tall should his map be?
- Cylindrical Projection The map maker in Problem 1 places the $y$-axis ($0^°$ longitude) at the center of the map as shown in Figure 2(b). Find the $x$- and $y$-coordinates of the following cities on the map.
- Seattle, Washington; $47.6^°$ N, $122.3^°$ W
- Moscow, Russia; $55.8^°$ N, $37.6^°$ E
- Sydney, Australia; $33.9^°$ S, $151.2^°$ E
- Rio de Janeiro, Brazil; $22.9^°$ S, $43.1^°$ W
- Stereographic Projection A map maker makes a stereographic projection of the southern hemisphere, from the south pole to the equator. The map is to have a radius of $20$ in.
- What value of $R$ should he use in the stereographic projection formulas?
- Find the polar coordinates of Sydney, Australia ($33.9^°$ S, $151.2^°$ E) on his map.
5-6 ◼ The cylindrical projection stretches distances between points not on the equator—the farther from the equator, the more the distances are stretched. In these problems we find the factors by which distances are distorted on the cylindrical projection at various locations.
- Projected Distances Find the ratio of the projected distance on the cylinder to the actual distance on the sphere between the given latitudes along a meridian.
- Between $20^°$ and $21^°$ N latitude
- Between $40^°$ and $41^°$ N latitude
- Between $80^°$ and $81^°$ N latitude
- Projected Distances Find the ratio of the projected distance on the cylinder to the distance on the sphere along the given parallel of latitude between two points that are $1^°$ longitude apart.
- $20^°$ N latitude
- $40^°$ N latitude
- $80^°$ N latitude
7-8 ◼ The stereographic projection also stretches distances—the farther from the south pole, the more distances are stretched. In these problems we find the factors by which distances are distorted on the stereographic projection at various locations.
- Projected Distances Find the ratio of the projected distance on the plane to the actual distance on the sphere between the given latitudes along a meridian.
- Between $20^°$ and $21^°$ S latitude
- Between $40^°$ and $41^°$ S latitude
- Between $80^°$ and $81^°$ S latitude
- Projected Distances Find the ratio of the projected distance on the plane to the distance on the sphere along the given parallel of latitude between two points that are $1^°$ longitude apart.
- $20^°$ S latitude
- $40^°$ S latitude
- $80^°$ S latitude
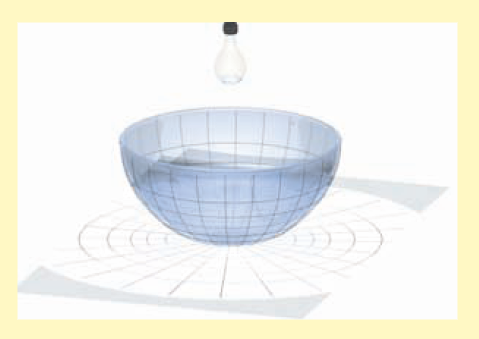
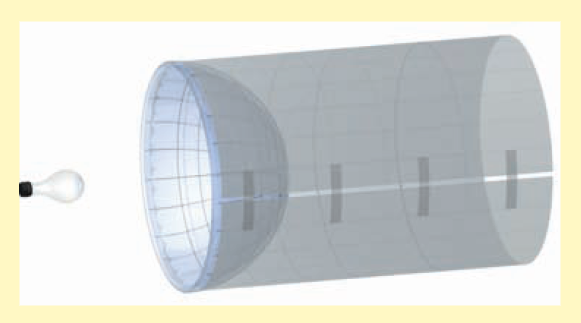
- Lines of Latitude and Longitude In this project we see how projection transfers lines of latitude and longitude from a sphere to a flat surface. You will need a round glass bowl, tracing paper, and a light source (a small transparent light bulb). Use a black marker to draw equally spaced lines of latitude and longitude on the outside of the bowl.
- To model the stereographic projection, place the bowl on a sheet of tracing paper and use the light source as shown in the figure.
- To model the cylindrical projection, wrap the tracing paper around the bowl and use the light source as shown in the figure.
- Other Projections There are many other map projections, such as the Albers Conic Projection, the Azimuthal Projection, the Behrmann Cylindrical Equal-Area Projection, the Gall Isographic and Orthographic Projections, the Gnomonic Projection, the Lambert Equal-Area Projection, the Mercator Projection, the Mollweide Projection, the Rectangular Projection, and the Sinusoidal Projection. Research one of these projections in your library or on the Internet and write a report explaining how the map is constructed, and describing its advantages and disadvantages.